跳表 SkipList
为什么会有跳表结构?
我们都知道实际上在做AVL(平衡二叉树)为了要保证平衡的效果往往会需要将树结构不断的做调整 (左旋、右旋等等,当然我们还知道这衍生出红黑树这种较高明的妥协产物),这种调整如果不遵循值递增等特殊的处理,往往会消耗大量的资源来做调整保证平衡效果维持log₂N的查询效率。但实际使用时候,自然的不可能说每一个场景都这么完美符合递增的效果,在这种情况下,跳表就诞生了,跳表的存在其实约等于在AVL和普通List之间找到一个平衡,保证了较高性能的查询和不太需要复杂的调整的一种数据结构。
提出人是William Pugh,原论文如下:Skip Lists: A Probabilistic Alternative to Balanced Trees
论文先介绍了跳表的结构,然后介绍一下怎么搜索、修改,介绍了搜索性能以及花了较长篇幅为什么他推荐用1/2的抽取率
跳表结构
为了方便后续的理解,这里稍微引入一下论文中的一张关键的图:
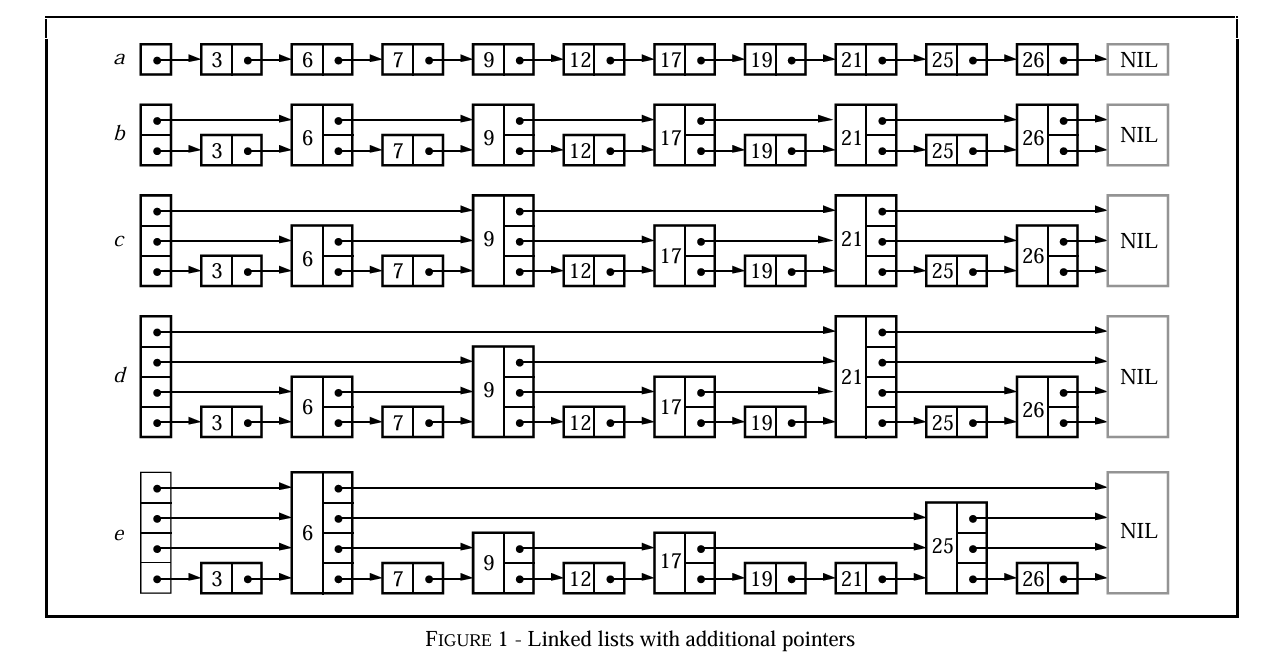
从这张图我们其实就可以大概知道,首先跳表是基于链表结构的,而从全局来看跟B+树的结构非常类似,从逻辑上最底层会包含有所有的数据值,从最底层 (第一层) 的结构往上找就可以看到逐渐稀疏 (从最顶层每往下一层都比上一层多 50%的节点 2 -> 4 -> 8 ······ [当然实际的抽取率是可以调整的] 也因此从他这张图可以知道查询效率也是近似于 log₂N)
层级构成
有一些介绍提供的图过于离谱,看起来都是完美抽取点,但实际上跳表的抽取是每一个节点都有 1/2 的概率成为上一层的节点,并可能构成出从整体来看奇形怪状的结构。实际的查询效率并不是完美的标准的 O(log₂N),而是取决于抽取点并决定于最后抽取结果。
所以它的最坏情况下的查询效率是 O(n) ~ O(log₂N) ,这也是为什么我说他是 LIst 和 AVL 之中的一种平衡算法结构。
而他的这种优化方式其实本质上就是利用概率抽取花一定的空间换取时间,由于概率抽取的效果,每一个节点都有可能抽取到,在极端场景下就会出现某一层抽取结束跟原层元素完全一样的情况。也因此实际上每一种基于跳表做实现实际存在的数据结构都会对最大层数做限制。例如ConcurrentSkipListMap就现在为62个层级节点,在Redis的SortedSet之中也有所使用,而在Redis之中限制的层数则是32层、抽取率是1/4 0.25。
跳表的特点
- 适合内存场景
- 跳表本质其实是基于链表结构实现的,其中Node本身可以分散在不同的内存区域
- 跳表的随机抽取特点导致他的层级容纳量不稳定,且为了保证层级可控一般还会对其进行限制 (不适合大量数据存储)
- 查询性能明显高于普通的List (牺牲一定内存空间换来的)
- 并发控制上表现更好
比AVL好在哪里?差在哪里?
对比AVL来说来说主要好在两个层面:
- 跳表结构不需要像 AVL 一样需要频繁的调整,带来性能损耗,只有因为增加元素或者删减元素的时候,才有可能会增加 / 减少层级带来调整方面的性能损耗问题
可以简单记忆为:跳表相比于AVL在修改方面有着更高的性能,但查询性能小于等于AVL - 跳表结构相比于树型结果更加适合尝试通过非锁算法来实现线程安全
详情请参考:ConcurrentSkipListMap/Set的实现
为什么Redis SortedSet要用SkipList?
- SkipList更适合内存场景:前面在介绍跳表的优点时已经提到,SkipList本身是链表的设计使得他更适合内存的环境,并且由于Redis作为内存数据库的设计基础。
- 开销可预估:SkipList的设计决定了他的内存开销是相对来说比较可控的 (特别是Redis既做了抽取率的降低,也做了最大层数的限制)
- 内存数据库频繁修改:如果用红黑树 / AVL 容易造成损耗
为什么关系型数据库不适合用SkipList?
众所周知,关系型数据库常用的算法数据结构式B树,而采用B树的关键其实是因为在B树中一个节点可以容纳众多子节点,使得他甚至在树型结构中都是“繁枝茂叶”的一类,这种设计的本质其实是为了一件事:能在更少的层级容纳更多的数据,从而降低磁盘IO的次数,借此提高性能。
而SkipList正如上文所提,实际上他存储空间利用率相比于标准的树型结构来说并不高,而且相对于B+树来说,如果将SkipList用于实际存储大量数据,那么必然会需要多次的磁盘IO来实现查找,如果考虑上跳表的随机抽取的特点,这个问题就更加明显了。
